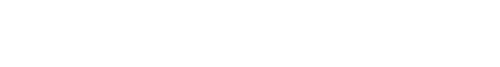数学の世界には、ときどき私たちの直感をくすぐる“不思議な現象”が現れます。今回取り上げるのは、SNS などでも人気のある 「π=4 の証明(?)」 と呼ばれる有名なパラドックスです。
もちろん、π(パイ)は 3.14159… のままで、4 になることは絶対にありません。 では、なぜそんな“おかしな結論”が導かれてしまうのでしょうか?
数学の本質である「極限」の考え方に触れながら、スッキリ解説していきます。
1. 問題の図形:半径 2 の 1/4 円
次のような図を考えます。
- 正方形 ABC(1 辺 2)
- 中心 C、半径 2 の 1/4 円弧 AB
この赤い円弧 AB の長さは、当然
2 × 2 × π × 1/4 = π
です。ここまでは誰も文句なしですね。
2. 円弧を「階段状の折れ線」で近似していく
つぎに、円弧を青い「階段状の折れ線」で近似してみます。折れ線を何段に分けても、
- 横方向の長さの合計:2
- 縦方向の長さの合計:2
なので、折れ線の総延長は
2 + 2 = 4
のまま。これは段数を増やしても絶対に変わりません。
3. 階段の段数を増やすと、なぜか円弧に近づく
折れ線の段数を増やしていくと、見た目はどんどん円弧に近づいていきます。
円弧との“すき間”の面積も、限りなく 0 に近づきます。
すると、ちょっと意地悪な発想が出てきます。
「面積が 0 になるなら、円弧と折れ線は一致するのでは?」
→「一致するなら長さも同じはず!」
→「円弧の長さ π と折れ線の長さ 4 が一致」
→ π=4!?
数学界が揺らぐ大事件……のように見えます。
4. どこが間違いなのか:核心部分
結論を先に述べると、
面積が 0 に近づくことと、曲線として一致することはまったく別物。
これがすべてです。
もっと身近な例を出すと、関数 y = 1/x を思い出してください。
limx→∞ (1/x) = 0
これは「0 に近づく」だけであり、グラフが x 軸に触れるわけではありません。
階段の折れ線と円弧の関係もまさに同じです。
5. なぜ長さが違うままなのか
階段状の折れ線の性質
- どれだけ細かくしても「水平線と垂直線」の組み合わせ
- 各方向の長さの合計は 2 と 2 のまま
- つまり構造的に「折れ線」でしかない
円弧の性質
- 傾きが少しずつ滑らかに変化する“曲線”
- 曲線の長さは π
階段が限りなく円弧に近づいても、「折れ線である」という性質は永遠に変わりません。
そのため、長さは常に 4 のままなのです。
6. 数学的まとめ
- 図形の「見た目の収束(点ごとに近づく)」
- 曲線長の収束(長さが一致する)
は、全く別の概念です。
折れ線は円弧に「点では近づく」が、曲線としての滑らかさがないため、長さの極限は 4 のままです。
したがって、
π = 4
などという結論は生まれません。
7. おわりに:数学の面白さは“限界”に宿る
このパラドックスは、極限の考え方の繊細さを体験する最高の題材です。
「近づくこと」と「一致すること」が違う。数学は、そんな当たり前のようで奥深い世界に支えられています。
疑問を持つことは、理解の第一歩。今回のような“ちょっと不思議な話”に出会ったときこそ、一歩立ち止まって考えてみると、数学が一段と面白くなりますよ。