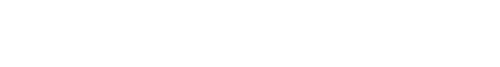SNSで話題になっていた図形問題に、「この問題は 1辺×1辺×0.57 で終わり」というコメントが付いていることがあります。
たしかに速い。でも、千尋進学塾としては「0.57を“呪文”にしない」ことが大切だと思っています。
結論:0.57の正体は (π−2)/2
あの「0.57」は、ざっくり言えば次の数の近似値です。
(π−2)/2 ≒ 0.5708…
つまり、円周率πが入った「面積の割合」が正体です。
0.57が使える理由(考え方の芯)
図の赤い部分は、半径が正方形の一辺と同じ円を2つ描いたときの重なり(レンズ形)です。
このレンズ形は、次の組み合わせで作れます。
- 90°の扇形が2つ
- そこから直角二等辺三角形が2つ引かれている
よって面積は
(扇形2つ)−(三角形2つ)
となり、整理すると
レンズ形の面積 =(正方形の面積)×((π−2)/2)
だから「1辺×1辺×0.57」が成立します。
ここから本題:小学生の“普通の解法”はどうする?
「0.57」解法は確かにアリ。でも、小学生が最初からこの比を持っていることは普通ありません。
では、小学生が“普通に”辿りつくにはどう教えるか。ポイントは次の2つです。
- ① 図形を分解する(扇形と三角形に見えるようにする)
- ② 使う公式は“いつもの公式”だけにする(扇形・三角形)
小学生の解法(王道):扇形−三角形で作る
正方形の一辺を8cmとします(問題図と同じ)。
ステップ1:円弧の中心を意識すると、赤い部分は90°の扇形が2つでできていると見えてきます。
ステップ2:ただし扇形だけだと赤い部分より大きいので、余分なところを引きます。余分な部分は、脚が8cmの直角二等辺三角形が2つです。
ステップ3:面積を計算します。
- 半径8cmの90°の扇形1つ:(1/4)×π×8×8
- それが2つ:(1/2)×π×8×8
- 直角二等辺三角形1つ:(1/2)×8×8
- それが2つ:8×8
よって赤い部分は
(1/2)×π×8×8 − 8×8
整理して
32π − 64(cm²)
となります。
※小数で答える必要があるなら π=3.14 として
32×3.14−64=100.48−64=36.48(cm²) です。
「0.57」は“ショートカット”。でも王道から生まれる。
ここまでが小学生の普通の解法(王道)です。
そして、この王道を一般化すると、
レンズ形=(正方形)×((π−2)/2)≒(正方形)×0.57
という「0.57ショートカット」に繋がります。
つまり、0.57は“突然降ってくる魔法”ではなく、中学受験用に王道の計算をまとめたものです。
千尋進学塾としての感想:「1つありだな」
ここからは私の感想です。
結論は、「1つありだな」です。
「数学はひらめきが大事」とは言いますが、ひらめくことができるのは1000人に1人もいません。
一方で、「高校生の数学は暗記」という先生もいます。
数学がめちゃくちゃ得意な方はどうやっても構いませんが、どこかで限界が来ます。
私の考えはこうです。
解法を暗記して、それらを組み合わせて使う延長上に、ひらめきがある。
これは、小学生の算数でも同じです。
- まずは王道(扇形−三角形)を理解して解けるようにする
- 次に型としてまとめ、速く処理できるようにする(0.57のような比)
- そして型のストックが増えると、初見でも組み合わせで戦えるようになる
この流れができると、入試本番で「見たことない!」となりにくい。
ひらめきは、天からの贈り物というより現場で鍛えた“編集力”に近いと思っています。
まとめ:速さと理解、どちらかではなく両立
- 小学生の王道:扇形−三角形で面積を作る
- 0.57の正体:(π−2)/2 を小数化した面積比
- 塾の方針:王道で理解 → 型で高速化 → 組み合わせで初見対応
千尋進学塾では、「答えが合う」だけでなく、なぜそうなるかを説明できる状態を目標に指導しています。
必要な処理力は鍛えます。ただし、処理を“呪文”にはしません。
📚「差のつく!読解のチカラ育成講座シリーズ」記事一覧
- ① “国語が苦手”は勘違い?読解力の正体、教えます
- ② “読めてるつもり”が一番危ない!読み飛ばし世代に欠けている力
- ③ 応用問題が解ける子の秘密は“読む力”にあった!
- ④ 読解力は国語だけの話じゃない!算数・理科にも効く“読みの技術”
- ⑤ 説明文が苦手な子に足りないのは“読書”じゃなく“論理力”
- ⑥ 小論文・推薦入試で差がつく!読解力×論理力の真価とは
- ⑦ 本を読むだけでは“読解力”は育たない?間違った読解力の鍛え方
- ⑧ “選択肢の消去法”で点が取れない子へ。論理的に読む力、ついてますか?
- ⑨ 読解力は“後からでも”伸ばせる?苦手意識をひっくり返す塾のトレーニング
- ⑩ 読解力と成績の相関関係|トップ層が必ず持っている“読みの技術”