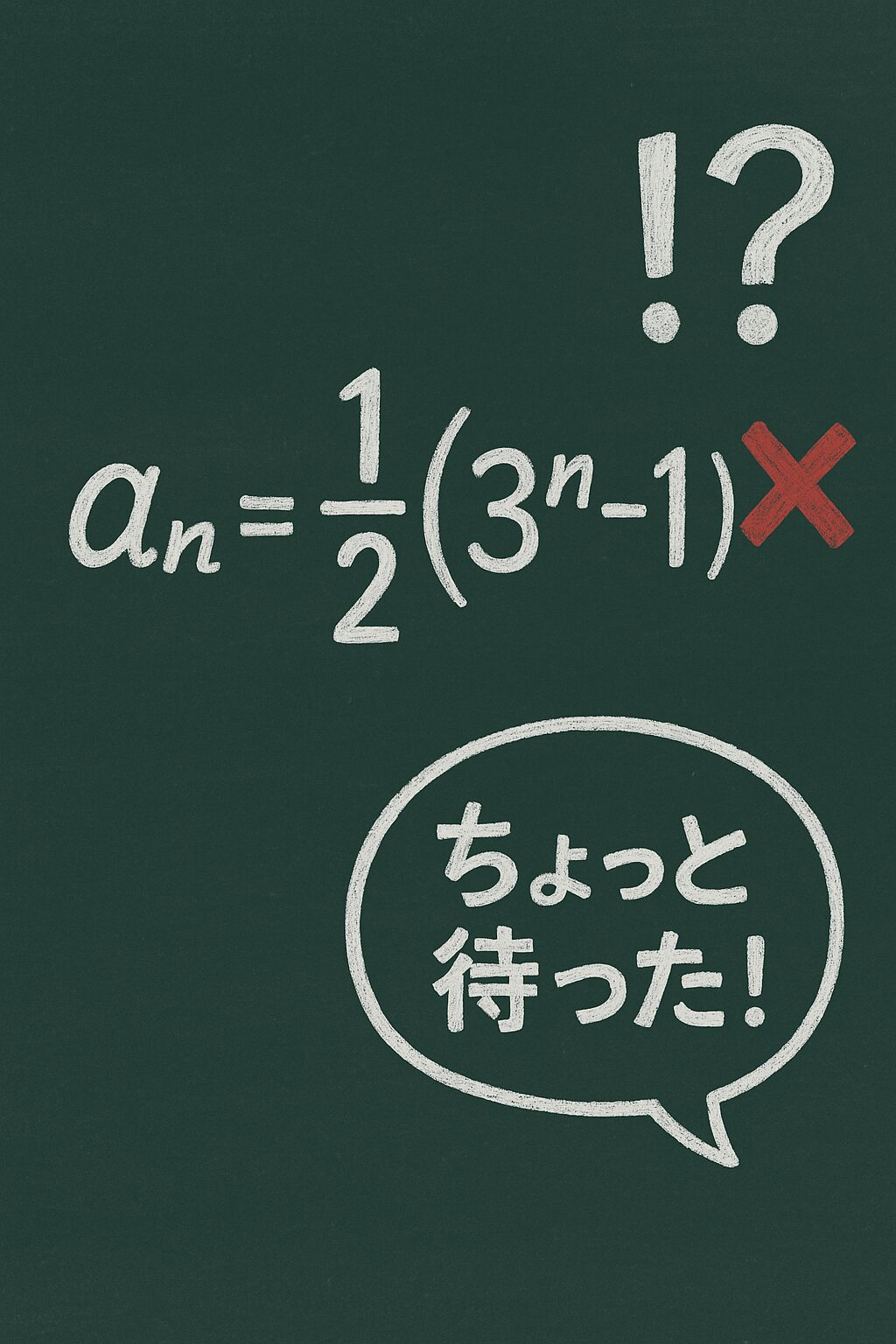【高校数学】aₙ₊₁＝aₙ＋3ⁿ の一般項でよくある間違い｜等比数列の公式ミスに注意！

最近、授業中にとても面白いやり取りがありました。
数列の一般項を求める問題で、生徒が次のような式を書いてきたのです。

aₙ = 1/2(3ⁿ - 1)

一見それっぽい。
計算結果も、a₁＝1、a₂＝4、a₃＝13…と、正しく見える。
でも――実は、これは完全な偶然の一致による「誤答」なんです。

---

与えられた漸化式

問題はこうでした。

• 初項：a₁ = 1
• 漸化式：aₙ₊₁ = aₙ + 3ⁿ

このとき、一般項 aₙ を求めよ。

---

正しい導き方

これは「加法型漸化式」と呼ばれるタイプで、前の項に何かを毎回足していく構造です。

書き出してみましょう。

a₁ = 1

a₂ = 1 + 3¹

a₃ = 1 + 3¹ + 3²

a₄ = 1 + 3¹ + 3² + 3³

…

aₙ = 1 + 3¹ + 3² + … + 3ⁿ⁻¹

ここで出てきたのが「3¹から3ⁿ⁻¹まで」の等比数列の和。

公式にあてはめて：

aₙ = 1 + 3 × (3ⁿ⁻¹ − 1)/(3 − 1) = (3ⁿ − 1)/2

これが正解です。

---

では、なぜ「1/2(3ⁿ − 1)」が間違い？

この式は「3⁰から3ⁿ⁻¹まで足した場合」に使う形です。

しかし今回の数列は「3¹から」なので、項数が1つ少ないし、初項も違う。

つまり、

• ✔️ 項数のカウントミス
• ✔️ 初項を3⁰=1と見誤っている

というダブルミスが発生しています。

---

もう一つのよくある間違い：「1/2(3ⁿ⁻¹ − 1)＋1」

これも実際にあった解答です。

これを書いた生徒の気持ちはよく分かります。
「1＋等比数列の和」という意識があるのは素晴らしい。
でも、計算が噛み合っていない。

具体的に：

n = 3 のとき

誤答：1/2(9 − 1) + 1 = 4 + 1 = 5

正解：(27 − 1)/2 = 13

⇒ 全然違います！

このミスは、「3から始まる等比の和なのに、公式をそのまま使ってしまった」ことによるもの。
公式は便利ですが、条件に合わせて調整しないと間違えるのです。

---

生徒にどう伝えるか？〜実際の指導場面から〜

1．「公式は中身を確認してから使うもの」

「この公式、初項いくつ用だっけ？」
「3⁰から？ 3¹から？ どこからどこまで足してる？」

2．図や表で項の並びを可視化する

a₁ = 1
a₂ = 1 + 3¹
a₃ = 1 + 3¹ + 3²
a₄ = 1 + 3¹ + 3² + 3³
          ↑ここがラスト

3．ちょっと笑える例えで印象づける

• 「この数列は“3の先払い”じゃなくて“3の後払い”やぞ」
• 「3⁰は“未払い”やから、足しちゃダメ」
• 「公式にぶち込む前に“数列の身分証明書”を確認！」

---

まとめ：公式より「状況の読み取り」が大事！

今回のような加法型の漸化式では、
公式の丸暗記よりも「どこからどこまで足してるか」が命です。

数列を“見る”ことに慣れてくると、ミスは自然と減っていきます。

---

千尋進学塾では「ミスを深掘りして学びに変える」指導を行っています

ただの正解・不正解だけで終わらせず、
「なぜ間違えたか」「その考えはどこまで合ってたか」を丁寧に確認。

生徒自身が「次はこう考えればいいんだ」と納得できる指導を行っています。

---

📲 お問い合わせ・無料体験はこちらから！

お気軽にLINEでご相談ください。
▶ LINEで質問・相談する

---

✏️ 関連記事はこちら

• 桑名高校1年生｜論理表現（英文法）の学習法｜感覚で身につける「ことば」としての英語力
• 桑名高校・川越高校1年生へ｜期末テストの山場「二次関数」の攻略法
• 桑名高校1年生｜数学Aの期末テスト対策ポイントを徹底解説！
• 桑名高校1年生｜数学Ⅰの1学期期末テスト、どこがポイント？塾から見た出題傾向と対策
• 桑名高校2年生｜1学期期末テストの範囲が発表されました（2025年）
• 【桑名高校】校舎の海抜は？避難所としての役割と安全性を徹底解説
• 漸化式が苦手な人へ｜才能じゃない、“型”と“努力”で勝てる数学
• 川越高校2年生の期末テスト範囲まとめ｜保護者が知っておきたい7つの注目ポイント【三重県立高校】